Apuntes programación lineal

En el siguiente enlace tenéis los apuntes de teoría sobre programación lineal y ejemplos.

Apuntes programación lineal

El ejemplo ha sido extraído de esta página en Vitutor y hay varios problemas propuestos para practicar en este mismo sitio:

• Problemas programación lineal (1)
• Problemas programación lineal (2)

"cuentas" para resolver los ejercicios 24 (103), 3b y 4a (91)

En el siguiente enlace tenéis  las "cuentas" para resolver los ejercicios 24 (p 103), 3b y 4a de la p. 91.

He usado la pagina matrixcalculator cuyo enlace está en los enlac e sútiles de bachillerato en la pestaña correspondiente.

Soluciones a lo ejercicio 4a mediante matrixcalc

ejercicio 24

ejercicio 25

Soluciones de sistemas no lineales y ecuaciones logarítmicas y expoenciales

En el documento pdf siguiente están las soluciones completas de algunos sistemas no lineales y ecuaciones logarítmicas y exponenciales. Exactamente son las de los ejercicios 2 y 3 (p 88), así como ls soluciones de los ejercicios 13 y 14(p 86) de la Unidad 3 del libro.

Solución completa sistemas no lineales y ecuaciones logarítmicas y exponenciales

Problemas de sistemas de ecuaciones y matrices de la PAU

En el siguiente documento pdf hay varios problemas sobre sistemas de ecuaciones, álgebra de matrices y discusión de sistemas extraídos de exámenes de la PAU de los últimos años:

Problema, sistemas y matrices

Exámenes de 2º bach CCSS curso 2015-16

Por orden de aparición los exámenes del curso pasado son:

• Probabilidad y estadística 
• Método de Gauss y álgebra de matrices
• Determinantes, Rocuhe-Frobenius y Programación lineal
• Límites y derivadas
• Derivadas y gráficas
• Integrales

Inicio del otoño

Hoy es el último día del verano. Y sabemos que el otoño empieza en el año 2016 el día 22 de septiembre (no el 21) e incluso sabemos la hora y el minuto:

Astronomia: inicio de las estaciones (IGN)

Esta hora límite no es una cuestión de temperaturas, sino de matemáticas y astronomía (mecánica celeste) que se puede calcular exactamente:

Inicio astronomico del otoño

Solución a los problemas de probabilidad (ampliación de matemáticas 3º ESO)

Los problemas de probabilidad que se han resuelto en clase han sido: 1, 4, 6, 7 , 8, 9 y 16.

Para realizar todos estos ejercicios se usa la ley de Laplace 

P = N. casos favorables/N. Casos totales 

 y para algunos ejercicios son útiles dos herramientas para organizar los datos: Cuadro de doble entrada (1, 6, 7, 10 y 16) y diagrama de árbol (8 y 9).

El método usado para solucionar estos problemas no necesariamente coincidirán con los expuestos en clase.

Solución problemas probabilidad

Exámenes de 4ª ESO del curso 2015-16

Aquí os dejo los exámenes de 4º de la E.S.O .del curso 2015-16 para que podáis practicar a los que os haga falta antes de los exámenes finales o de septiembre.

• Unidad 1  
• Unidad 2 (mezclas, modelos atómico y formulación) 
• Unidad 3
• Unidad 4
• Unidad 5
• Unidad 6
• Unidad 7
•  Unidad 8-9

Ánimo y suerte.

flobo@educa.madrid.org

Resultados finales de los ejercicios del jueves 2 de junio

Voy a poner aquí los resultados de las cuentas de los ejercicios 10 y 11 de la página 255 del libro. Las fórmulas ya las tenéis, lo único que queda es usar la calculadora.

10. Calcula las siguientes probabilidades si x-> B(7;0,4)

• a) P[x = 2] = 0,261
• b) P[x = 5] = 0,077
• c) P[x = 0] = 0,028
• d) P[x > 0] = 1 - P[x = 0] = 0,972
• e) P[x > 3] = 0,290
• f) P[x > 5] = 0,904  (Al final tenía razón Paula)

11. Calcula las siguientes probabilidades si x-> B(9;0,2)

• a) P[x < 3] = 0,738
• b) P[x >= 7] = 0,000314
• e) P[x <= 9] =1 (Suceso seguro)
• f) P[x >= 9] =P[x = 9] = 0,000000512

Exámenes de 1º Bachillearto CCSS curso 2015-16

Aquí os dejo los exámenes de 1º de bachillerato del curso 2015-16 para que podáis practicar a los que os haga falta.

• Números reales 
• Polinomios, ecuaciones y sistemas 
• Gauss y funciones
• Límites y derivadas. Aplicaciones de las derivadas
• Estadística y probabilidad 

flobo@educa.madrid.org

El nuevo icono del blog

Pues aquí está:

Es un regalo de parte de mis alumnos de 2º de bachillerato de este curso.

Muchas gracias.

Nueva información en la página Enlaces PAU

Acabo de añadir hiperenlaces a páginas y libros con problemas resueltos de los exámenes de la PAU de los últimos años. Aprovechadlos y comprobadlos, apuntad las dudas y me hacéis las preguntas pertinentes el día que nos reunamos.

flobo@educa.madrid.org

Solución a losproblemas de recuento (ampliacion de matematicas 3º ESO)

Ya hemos acabado todos los problemas útiles y accesibles de recuento. Recordad que la única fórmula importante es

N = n1·n2·n3 ···

dónde n1 es la cantidad de opciones que hay en la primera elección, n2 la cantidad de opciones d el asegunda elección, etc...

Si estamos hablando de la cantidad de reordenaciones de n elementos entonces usamos el factorial

n! = n·(n-1)·(n-2)···2·1

Lo que en realidad es un caso particular de la fórmula general anterior.

Algunas explicaciones del libro son algo distintas a las que os di en clase, como seguro que tenéis unos apuntes completos y claros, usad ambos tipos de explicaciones para entender mejor la respuesta.

Los problemas resueltos en clase han sido por este orden: 7, 9, 1, 8, 11, 2, 4 y 6

Soluciones problemas recuentos

Soluciones de ejercicios de la unidad 7 de 1º bachillerato

En el fichero pdf que esta más abajo tenéis una fotocopia de los ejercicios de las páginas 177 y 178 del libro de texto. En esta fotocopia están los enunciados y al lado, escrito a mano, las soluciones. En algún límite en el que sea necesario calcular los límites laterales, he puesto las soluciones en una llave siendo el resultado de arriba el límite por la izquierda y el de abajo el límite por la derecha.

Haced todos los ejercicios que podáis, compradlo con estas soluciones y comproba los resultados discordantes, preguntándome si no entendéis el resultado, o el error cometido.

Solución de los ejercicios del 1 al 23 (p 177-178) sobre continuidad y límites (U7)

Límites infinitos en funciones polinómicas y racionales

Existe un criterio que permite calcular fácil mente un limite de una función polinómica o racional:

Si x tiende a infinito (o a - infinito) aproximamos las función polinómica por su término principal y la función  racional por el cociente de sus dos términos principales (uno en el numerador y otro en el denominador).

Resumiendo si x tiende a infinito nos quedamos solo con los términos principales.

¿Por qué? Porque cuando x toma valores cada vez más grandes son los términos de mayor grado los que más contribuyen al resultado del cálculo de la fórmula, por lo tanto, para un valor de x suficientemente grande el término principal nos da el resultado de la fórmula con un error pequeñísimo.

Se pueden ver un par de ejemplos, una función polinómica y otra racional en estos archivos:

• Límites infinitos de funciones polinómicas y racionales (pdf)
• Límites infinitos de funciones polinómicas y racionales (xls)
•  Límites infinitos de funciones polinómicas y racionales (ods)

Las sucesiones de las que hable en la última clase [3ºESO ampliación]

El último día de clase antes de las vacaciones de Semana Santa hablamos de sucesiones y os dejé tres sucesiones de las que había que deducir el siguiente término a partir de los términos ya conocidos.

En cierta manera calcular el siguiente término de una sucesión se parece al método científico. Hay que  buscar una propiedad común a todos los términos conocidos o un procedimiento que nos dé un término a partir de los anteriores, hacer una hipótesis, comprobarla, y si todo va bien, hacer la predicción.

Seguro que podéis buscar (y encontrar)  estas series en Google pero lo divertido es pensar, no tener la solución.

Sucesión 1: 2,10,12,16,17,18,19,...

Esta ya la solucionasteis en clase. Para quién no estuviese atento o no lo viese la pista es que está serie sería distinta si hablásemos en inglés. Además hay dos soluciones igualmente correctas.

Sucesión 2: 1, 11, 21, 1211, ...

Sucesión 3: 2,6,42, ...

Buena Semana Santa.

flobo@educa.madrid.org

Modelo de diapositiva para el trabajo de Rocas (4º ESO)

Si pincháis en este enlace Descargar modelo PowerPoint 

El programa usado para la presentación es PowerPoint. En cada diapositiva modelo se puede insertar una foto, un título con el nombre de la roca, un texto con el tipo de roca(ígnea, sedimentaria o metamórfica) y un comentario mediano (4 o 5 renglones) sobre esta roca.

Los equipos pueden ser de dos o tres personas.

Os recuerdo que la fecha límite de entrega es el jueves 17 de marzo.

Cuando hayáis acabado el trabajo lo podéis enviar al siguiente correo: flobo@educa.madrid.org

Soluciones a los problemas 5 a 7 de "Tiempo, distancia y velocidad" [3 ESO ampliación ]

Aquí están las soluciones de los problemas del tema de "Tiempo, distancia y velocidad" del 5 al 7. Son los problemas solucionados en las clases del viernes 26 de febrero.
El problema n. 7, que trata sobre como un perro Centella alcanza a otro llamado Rayo está aquí resuelto en función de los dos parámetros m y h, tal y como está en el libro. En la última clase os propusé el mismo problema pero sustuyendo los parámetros m y h por números concretos. En particular m = 1,5 y h = 20 metros.

Soluciones problemas del 5 al 7 "Tiempo, distancia y velocidad"

flobo@educa.madrid.org

La solución correcta del ejercicio 10 pg 180 (2º Bach)

Definitivamente el enunciado del ejercicio 10 e (pg 180) es incorrecto en el sentido de que la solución de este ejercicio es demasiado complicada para el nivel de este curso y no coincide con la expuesta en el solucionario.

En particular, la ecuación de cuarto grado que aparece no se puede resolver factorizando por Ruffini.

Empecemos viendo la gráfica de la función:

Se puede ver que los extremos están entre 1 y 2 uno de ellos y el otro entre 3 y 4.  Esta claro queno se podrían obtener usando la regla de Ruffini. Se puede acceder a la página de la gráfica pinchando sobre ella.

Las soluciones exactas de esta ecuación $$x^4-6x^3+15x^2-28x+24=0$$  se pueden ver en esta página.

Soluciones a los problemas 1 a 4 de "Tiempo, distancia y velocidad" [3 ESO ampliación ]

Aquí están las soluciones de los problemas del tema de "Tiempo, distancia y velocidad" del 1 al 4. Son los problemas solucionados en las clases del viernes 23 y el martes 19 de febrero.

Soluciones problemas del 1 al 4 "Tiemo, distancia y velocidad"

flobo@educa.madrid.org

Ejercicio sobre transformaciones de funciones

Vamos a resolver aquí, de nuevo, el ejercicio 1 de la pagina 116 en el que teníamos que usar las distintas transformaciones de una curva al hacer pequeños cambios en la fórmula que define la función.
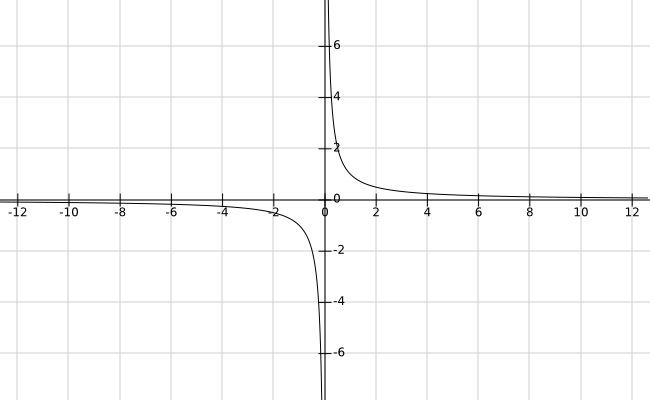
Primero dibujamos la función $$f(x)=\frac{1}{x}$$
Esta función es una función de proporcionalidad inversa o hiperbólica con asíntota horizontal y vertical en los ejes x e y con el punto x= 0 fuera de su dominio. Junto con estas ideas gráficas y, si es necesario, una tabla de valores nos sale la siguiente gráfica.

Si se pincha en la imagen saltamos a la página original con todos los parámetros.

 

Después tenemos la función $$g(x)=\frac{1}{x+3}$$

Evidentemente esta función es igual a f(x + 3). Se trata de sumar una constante a la variable x y esto implica en la gráfica un desplazamiento horizontal respecto de la gráfica anterior.

Dibujamos juntas las curvas de la función anterior y de esta para apreciar mejor la transformación gráfica. En color rojo la nueva función.

Después tenemos la función $$h(x)=-\frac{1}{x+3}$$

Evidentemente esta función es igual a - g(x). Multiplicamos por -1 la fórmula de la función anterior y esto implica que la nueva gráfica es el reflejo respecto del eje horizontal.

Después tenemos la función $$j(x)=-\frac{1}{x+3}+8$$

Evidentemente esta función es igual a h(x) + 8. Se trata de sumar una constante a la formula de la función anterior h(x) y esto implica en la gráfica un desplazamiento vertical respecto de la gráfica anterior.

Soluciones de los sistemas de ecuaciones por Gauss (Navidad))

En el siguiente enlace tenéis las soluciones de los sistemas de ecuaciones resueltos por el método de Gauss. Este camino no es el único posible, si llegáis a las mismas soluciones por un camino distinto pero correcto está bien.

Solución de los sistemas

Fijaos en las ecuaciones de los sistemas: el ejercicio 43 corresponde al 48, 49 y 50, y el ejercicio 44 corresponde al ejercicio 50.

Siempre hay que apuntar los pasos que dais y las operaciones que realizáis con las ecuaciones para llegar a un sistema escalonado.

Importante:
SI -> Sistema Incompatible (sin solución)
SCI -> Sistema Compatible Indeterminado (con muchas soluciones). Hay quie escribir dos de las incógnitas en función de la tercera.

3 ESO ampliación Soluciones a los problemas del 11 al 13 de proporrcionalidad

Aquí están las soluciones de los problemas de proporcionalidad del 11 al 13. Son los problemas solucionados en la clase del viernes 5 de Febrero.

Soluciones problemas del 11 al 13 

Y para aquellos que hayan perdido, o por algún otro motivo ignoto no encuentren alguna de las fotocopias que he repartido aquí dejó todas los enunciados de los problemas del libro que estamos usando en clase.

Problemas de Ampliación

Trabajad bien para el examen de este martes. Aún queda tiempo.

flobo@educa.madrid.org

3 ESO ampliación Soluciones a los problemas del 6 al 10 de proporrcionalidad

Aquí están las soluciones de algunos de proporcionalidad del 6 al 10. Son los problemas solucionados en la clase del viernes 29 de enero.

Soluciones problemas del 6 al 10

flobo@educa.madrid.org

3 ESO ampliación Soluciones a los problemsa de 3, 4 y 5 de proporrcionalidad

Aquí están las soluciones de algunos de proporcionalidad (3, 4 y 5). Son los problemas solucionados en la clase del viernes 22 de enero.

Soluciones página 33

flobo@educa.madrid.org

3 ESO Ampliación: Soluciones ejercicios de potencias yproporcionalidad

Aquí están las soluciones de los últimos ejercicios de potencias (11 y 12) y los primeros de proporcionalidad (1 y 2)

Soluciones página 32

flobo@educa.madrid.org

3 ESO Ampliación: soluciones ejercicios de potencias

sregún dije, a partir de ahora publicaré las soluciones de los problemas ya explicados y resueltos en clase. Esto no debería sustituir a los apuntes que tomáis en clase. Solo es una ayuda para que podáis completar y aclarar lo que no hayáis podido escribir en clase.

por lo tanto usad esto para completar los apuntes y solucionar dudas, pero siempre preguntando en clase lo que no esté suficientemente claro.

Además, lo que está en el libro no siempre tiene que coincidir al 100% con lo que se da en clase ya que las explicaciones del profesor son siempre una adaptación al alumnado.

Solución ejercicios de potencias

Para cualquier duda flobo@educa.madrid.org o en los comentarios

Ejercicios 8 de enero 4º ESO

Para aquellos que no lo apuntaron o no vinieron el día 8 de enero, aquí os dejo (sin que sirva de precedente) lo que habría que hacer para el lunes:

• Problemas 6, 7 y 8 pag. 81
• Sistemas de ecuaciones ej 1 (d,f ) y ej 2 (d,e) pag.  83

Teniendo en cuenta que este jueves tenemos examen de matemáticas, conviene hacer estos ejercicios que servirán en parte de repaso para este examen y podrán hacer aflorar dudas que convendrá resolver antes del jueves.

Por cierto, el lunes expliqué la resolución d elos sistema de ecuaciones por el método de sustitución y de reducción. Algo ya conocido del curso pasado.