Ejercicio sobre transformaciones de funciones

Vamos a resolver aquí, de nuevo, el ejercicio 1 de la pagina 116 en el que teníamos que usar las distintas transformaciones de una curva al hacer pequeños cambios en la fórmula que define la función.
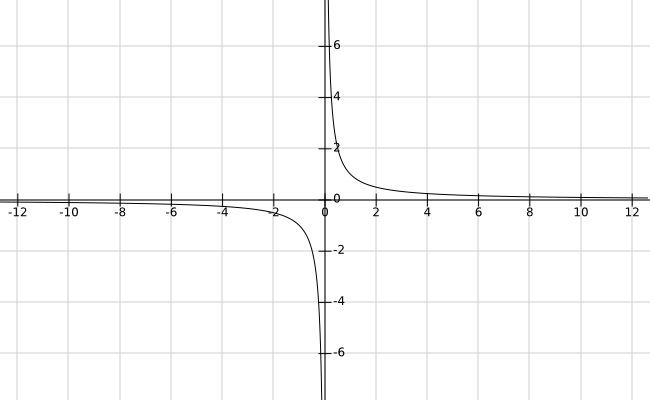
Primero dibujamos la función $$f(x)=\frac{1}{x}$$
Esta función es una función de proporcionalidad inversa o hiperbólica con asíntota horizontal y vertical en los ejes x e y con el punto x= 0 fuera de su dominio. Junto con estas ideas gráficas y, si es necesario, una tabla de valores nos sale la siguiente gráfica.

Si se pincha en la imagen saltamos a la página original con todos los parámetros.

 

Después tenemos la función $$g(x)=\frac{1}{x+3}$$

Evidentemente esta función es igual a f(x + 3). Se trata de sumar una constante a la variable x y esto implica en la gráfica un desplazamiento horizontal respecto de la gráfica anterior.

Dibujamos juntas las curvas de la función anterior y de esta para apreciar mejor la transformación gráfica. En color rojo la nueva función.

Después tenemos la función $$h(x)=-\frac{1}{x+3}$$

Evidentemente esta función es igual a - g(x). Multiplicamos por -1 la fórmula de la función anterior y esto implica que la nueva gráfica es el reflejo respecto del eje horizontal.

Después tenemos la función $$j(x)=-\frac{1}{x+3}+8$$

Evidentemente esta función es igual a h(x) + 8. Se trata de sumar una constante a la formula de la función anterior h(x) y esto implica en la gráfica un desplazamiento vertical respecto de la gráfica anterior.